Java 递归
递归是一种在编程中广泛使用且功能强大的技术,在 Java 语言中尤为常见。所谓递归,指的是在方法或函数的定义中直接或间接调用自身的过程。借助递归,能够有效解决某些复杂问题,简化代码结构,并实现高效的算法设计。
本文将系统介绍 Java 中递归的基本原理、常见应用场景与具体实现方式,并提供相应的示例代码以帮助理解。
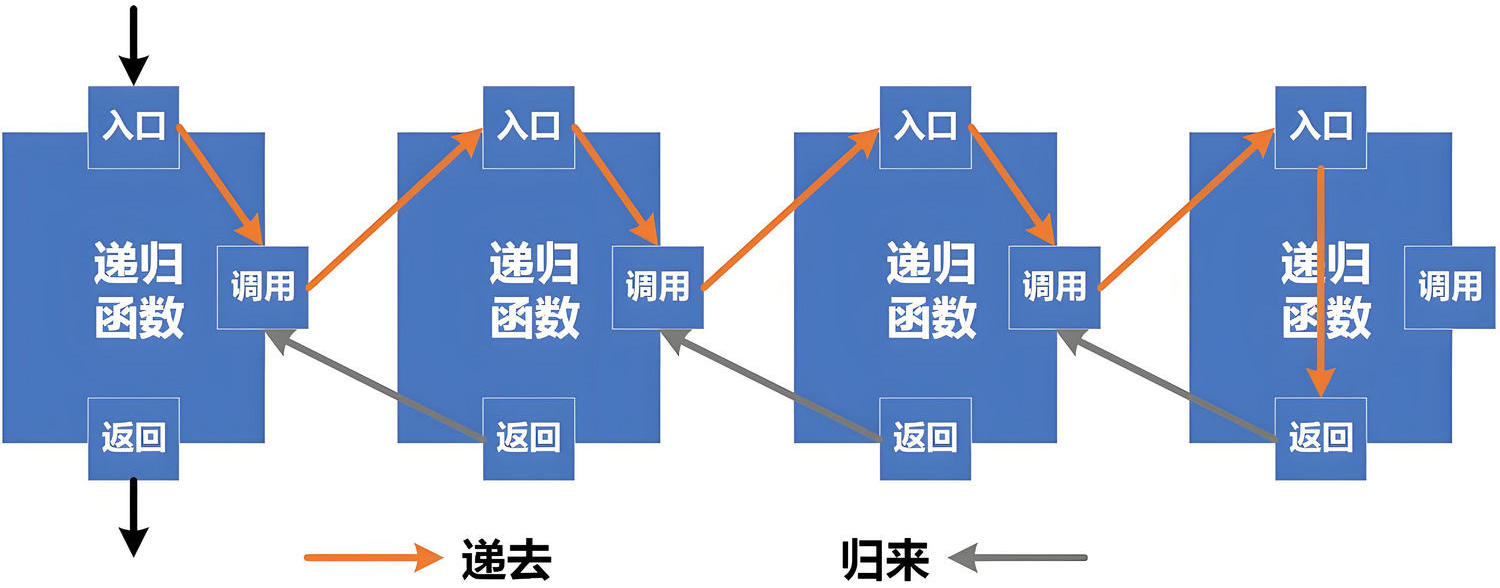
Java 递归原理
递归是基于函数调用栈的原理实现的。当方法被调用时,JVM 会在调用栈中为其分配一个栈帧,用于存储该方法的参数、局部变量及返回地址等信息。在递归调用过程中,方法会在其执行体内调用自身,从而使得多个结构相似的栈帧被依次压入调用栈。直到满足递归终止条件时,调用开始逐层返回,此时栈帧按相反顺序出栈,各次调用的结果被依次处理,最终完成整个递归过程。
递归的核心在于明确定义递归终止条件与递归调用条件。若缺少合适地终止条件,或是递归调用的条件设置不当,就会导致递归过程陷入无限循环,最终引发栈溢出错误。
JAVA 递归使用场景
递归在众多问题中都有重要应用,尤其适用于那些能够被逐层分解为规模更小的子问题的情况。
✅ 以下是一些常见地递归应用场景:
- 数学问题:例如阶乘运算、斐波那契数列求解等;
- 数据结构操作:包括二叉树遍历、链表反转等;
- 搜索和回溯算法:如深度优先搜索(DFS)、回溯算法等;
- 分治算法:典型如归并排序、快速排序等。
使用递归处理这类问题时,往往能够使代码逻辑更加简洁,同时提升可读性和可维护性。
Java 递归实现方式
在 Java 编程中,实现递归通常需要定义一个递归函数(方法)。递归函数的实现需要满足以下两个要素:
- 终止条件(Base Case):定义递归终止的条件,以防止无限递归的发生。
- 递归调用(Recursive Call):在方法内部调用自身,以处理规模更小的子问题。
✅ 下面通过一个经典的斐波那契数列求解问题来演示 Java 递归的具体实现方式:
public class Fibonacci {
public static int fibonacci(int n) {
// 终止条件:第0项为0,第1项为1
if (n <= 1) {
return n;
}
// 递归调用:当前项等于前两项之和
return fibonacci(n - 1) + fibonacci(n - 2);
}
public static void main(String[] args) {
int n = 6;
int result = fibonacci(n);
System.out.println("斐波那契数列第" + n + "项为:" + result);
}
}在上述代码中,fibonacci 方法通过递归实现了斐波那契数列的计算。方法首先检查输入参数 n 是否小于等于 1,以此作为递归的终止条件。如果满足该条件,直接返回 n 的值(即第0项为0,第1项为1)。否则,方法通过递归调用自身来计算第 n-1 项和第 n-2 项的和,从而得到第 n 项的值。
使用递归时需特别注意:必须确保终止条件能够被满足,且每次递归调用都应使问题规模向终止条件趋近,从而避免无限递归的发生。
Java 递归优缺点
递归作为一种重要的编程技术,在特定场景下具有独特优势,但也存在明显的局限性。
✅ 以下是 Java 中递归的主要优缺点分析:
1. 递归优点
- 简化问题:递归能够将复杂问题分解成更小规模的子问题,简化了问题的解决过程。
- 提高代码可读性:递归能够直观地表达问题的解决思路,提高了代码的可读性。
- 实现高效算法:递归在某些算法中能够实现高效的解决方法,如分治法等。
2. 递归缺点
- 栈溢出风险:递归可能导致方法调用栈过深,造成栈溢出错误。
- 性能损耗:递归调用需要创建多个栈帧,对系统资源有一定的消耗。
- 可能造成代码难以理解:递归的使用需要谨慎,过度使用可能使代码难以理解和调试。
因此,在使用递归时需要权衡其优缺点,并根据具体问题选择合适地解决方案。
反馈提交成功
感谢您的反馈,我们将尽快处理您的反馈

