机器学习（ML）训练回归模型

机器学习

学习即迭代：机器学习（Machine Learning）模型通过多轮数据训练优化获得。

每次迭代自动调整权重参数（Weight Values），当代价函数（Cost Function）不再下降时即完成模型训练。

多次训练，找到最佳的拟合直线：

100 次 200 次 300 次 500 次

尝试一下 »

梯度下降法

梯度下降法（Gradient Descent）是机器学习中最核心的优化算法，其核心思想是通过迭代调整参数，沿着目标函数（通常是代价函数）的负梯度方向逐步逼近最优解。

简单线性回归模型（Linear Regression Model ）可用于演示梯度下降法的原理。

线性回归的目标是为一组(x,y)数据点拟合最佳线性图形。虽然可通过数学公式直接求解，但机器学习算法同样能有效解决该问题。

上述示例正是通过梯度下降算法实现了线性回归的求解过程。

整个过程从散点图和线性模型（y = wx + b）开始，通过调整直线的权重（斜率）和偏置（截距）来训练模型，最终找到最拟合数据的直线。

以下是解决该问题（以及其他类似问题）的训练对象（Trainer Object）代码实现。

训练器对象

创建一个训练器对象（Trainer object），该对象可以在两个数组（xArr，yArr）中取任意数量的（x，y）值。

将权重值（weight）初始化为0，偏置项（bias）初始化为1。

需设置学习常数（learnc）并定义损失变量：

function Trainer(xArray, yArray) {
    this.xArr = xArray;
    this.yArr = yArray;
    this.points = this.xArr.length;
    this.learnc = 0.00001;
    this.weight = 0;
    this.bias = 1;
    this.cost;

代价函数

代价函数（Cost Function）是机器学习中用来衡量模型预测结果与真实值之间差异的函数。简单来说，它是一个告诉我们"模型预测有多糟糕"的评分标准。

想象你在一个靶场学习射箭。每次射箭后，都能看到箭矢离靶心的距离，这个"距离"就是类似于机器学习中的代价函数值——它客观量化了当前射击的准确度，反映了模型预测的误差程度。

代价函数基于线性回归模型的参数（权重系数w和偏置项b，对应模型表达式y=wx+b），通过系统评估拟合直线与训练数据点集的整体偏离程度，输出量化的预测误差值。

误差计算的具体方法是：遍历图中所有(x,y)数据点，累加每个数据点的实际y值与直线预测值之间的平方距离。

最常规的做法是对距离取平方（以确保值为正），同时使误差函数可微。

this.costError = function() {
    total = 0;
    for (let i = 0; i < this.points; i++) {
        total += (this.yArr[i] - (this.weight * this.xArr[i] + this.bias)) **2;
    }
    return total / this.points;
}

代价函数（Cost Function）又称误差函数（Error Function），该函数实际采用的公式如下：

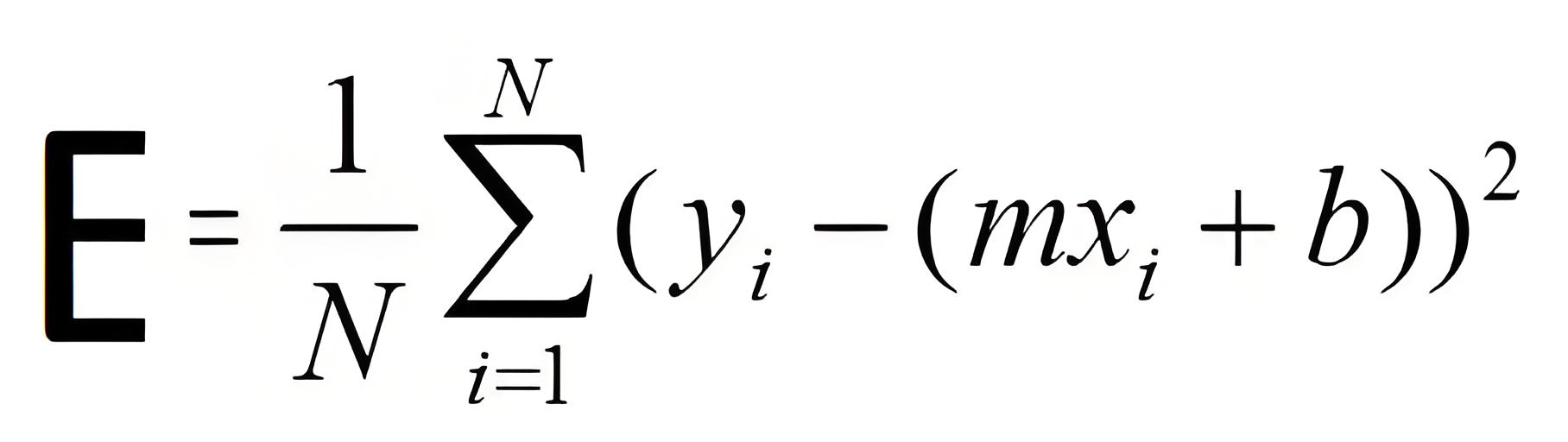
误差函数中各参数定义：

• E：误差值（代价）
• N：观测点总数
• y：各观测点的真实值（标签）
• x：各观测点的特征值
• m：斜率（权重）
• b：截距（偏置项）
• mx + b：模型预测值
• 1/N * ∑₁ᴺ：平方均值运算

训练函数

现在开始执行梯度下降算法。

梯度下降算法将驱动代价函数向最优拟合直线逼近。

每次迭代都将推动参数m和b向误差更小的拟合直线更新。

为此，我们添加一个训练函数，该函数会多次遍历全部数据集：

this.train = function(iter) {
    for (let i = 0; i < iter; i++) {
        this.updateWeights();
    }
    this.cost = this.costError();
}

权重更新函数

上述训练函数应在每次迭代中更新权重和偏置项。

参数更新方向通过以下两个偏导数计算确定：

this.updateWeights = function() {
    let wx;
    let w_deriv = 0;
    let b_deriv = 0;
    for (let i = 0; i < this.points; i++) {
        wx = this.yArr[i] - (this.weight * this.xArr[i] + this.bias);
        w_deriv += -2 * wx * this.xArr[i];
        b_deriv += -2 * wx;
    }
    this.weight -= (w_deriv / this.points) * this.learnc;
    this.bias -= (b_deriv / this.points) * this.learnc;
}

创建自定义机器学习库

库核心代码实现：

function Trainer(xArray, yArray) {
    this.xArr = xArray;  // 特征数组
    this.yArr = yArray;  // 标签数组
    this.points = this.xArr.length;  // 数据点数量
    this.learnc = 0.00001;  // 学习率
    this.weight = 0;  // 权重初始值
    this.bias = 1;  // 偏置项初始值
    this.cost;  // 损失值

    // 代价函数（均方误差）
    this.costError = function() {
        total = 0;
        for (let i = 0; i < this.points; i++) {
            total += (this.yArr[i] - (this.weight * this.xArr[i] + this.bias)) **2;
        }
        return total / this.points;  // 返回平均平方误差
    }

    // 训练函数
    this.train = function(iter) {
        for (let i = 0; i < iter; i++) {
            this.updateWeights();  // 迭代更新参数
        }
        this.cost = this.costError();  // 记录最终损失值
    }

    // 权重更新函数（梯度下降）
    this.updateWeights = function() {
        let wx;  // 临时计算变量
        let w_deriv = 0;  // 权重梯度
        let b_deriv = 0;  // 偏置梯度
        for (let i = 0; i < this.points; i++) {
            wx = this.yArr[i] - (this.weight * this.xArr[i] + this.bias);  // 误差计算
            w_deriv += -2 * wx * this.xArr[i];  // 权重偏导累计
            b_deriv += -2 * wx;  // 偏置偏导累计
        }

        // 参数更新（学习率调整步长）
        this.weight -= (w_deriv / this.points) * this.learnc;
        this.bias -= (b_deriv / this.points) * this.learnc;
    }
} // 训练器对象结束

现在您可以在HTML中引入该机器学习库：

<script src="myailib.js"></script>

尝试一下 »