弗兰克·罗森布拉特(Frank Rosenblatt)
弗兰克·罗森布拉特(1928-1971)美国心理学家,人工智能领域先驱。
1957年在康奈尔航空实验室使用IBM 704计算机开发出首个感知机(Perceptron)程序 → 实现模拟生物神经元的学习能力。
神经元通过电信号存储信息,并基于先前的输入做出决策。
弗兰克由此产生构想:感知机可以模拟大脑的这种运作机制,实现自主学习和决策功能。
感知机原理
最初的感知机被设计用于接收若干二进制输入,并产生一个二进制输出(0或1)。
其核心思想在于:通过为每个输入分配不同的权重来体现其重要性,仅当所有输入值的加权总和超过特定阈值时,才会触发"是/否"(真/假、0/1)的二元决策机制。
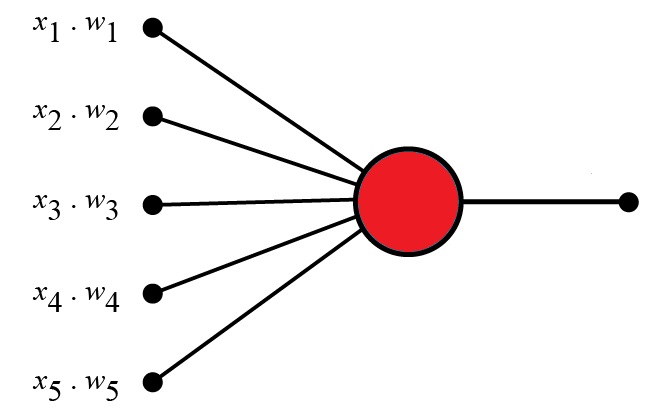
感知机示例
想象你的大脑中有一个感知机正在做决策:是否要去听这场演唱会?
它主要考量两个关键因素:艺人表演水平如何?当日天气状况是否理想?
那么,这两个影响因素的权重该如何设定才合理呢?
| 决策因素 | 输入值 | 权重 |
|---|---|---|
| 艺人表演水平 | x₁ = 0 或 1 | w₁ = 0.7 |
| 天气是否理想 | x₂ = 0 或 1 | w₂ = 0.6 |
| 朋友是否同行 | x₃ = 0 或 1 | w₃ = 0.5 |
| 是否提供餐饮 | x₄ = 0 或 1 | w₄ = 0.3 |
| 是否供应酒水 | x₅ = 0 或 1 | w₅ = 0.4 |
感知机算法
由弗兰克·罗森布拉特提出,算法步骤:设置阈值、所有输入值乘以对应权重、求和所有乘积结果、激活输出。
1. 设置阈值
阈值 = 1.5 # 决策临界值2. 计算加权输入
x₁ × w₁ = 1 × 0.7 = 0.7 # 艺人水平(重要)
x₂ × w₂ = 0 × 0.6 = 0 # 天气(不理想)
x₃ × w₃ = 1 × 0.5 = 0.5 # 朋友同行(有)
x₄ × w₄ = 0 × 0.3 = 0 # 无餐饮
x₅ × w₅ = 1 × 0.4 = 0.4 # 有酒水3. 求和所有乘积结果
加权和 = 0.7 + 0 + 0.5 + 0 + 0.4 = 1.64. 激活输出
if 加权和 > 1.5:
return "去演唱会" # 1.6 > 1.5 → 决定参加
else:
return "不去演唱会"提示:天气权重对你来说是0.6,但对别人可能不同。权重越高意味着天气对他们越重要。阈值对你来说是1.5,但对别人可能不同。阈值越低意味着他们更愿意参加任何演唱会。
感知机实例
下面通过一个感知机音乐会决策模拟器,来深化您对感知机的理解。
const threshold = 1.5;
const inputs = [1, 0, 1, 0, 1];
const weights = [0.7, 0.6, 0.5, 0.3, 0.4];
// 计算加权和
let sum = inputs.reduce((total, input, index) => {
return total + (input * weights[index]);
}, 0);
const activate = (sum > 1.5);感知机概念
感知机是一种人工神经元模型,其设计灵感来源于生物神经元的工作原理。作为人工智能领域的关键组件,它是构建神经网络的基础单元。核心组成要素:
1. 感知机输入系统
- 一个感知机可接收单个或多个输入信号
- 感知机的输入单元称为节点(Node)
- 每个节点都包含两个属性:输入值和权重值。
2. 节点数值(输入值)
- 数值范围:每个输入节点仅接受
1或0的二进制值 - 逻辑含义:
1→ 是/真/存在(True/Yes),0→ 否/假/不存在(False/No) - 节点值为:
1, 0, 1, 0, 1
3. 节点权重系统
- 权重分配:每个输入节点对应一个可调节的权重值
- 权重表示每个节点的强度
- 数值越大意味着该输入对输出的影响越强
- 节点权重为:
0.7, 0.6, 0.5, 0.3, 0.4
4. 加权求和计算
- 感知机对输入进行加权求和计算
- 感知机将每个输入值与其对应的权重相乘后求和
- 加权求和:
0.7*1 + 0.6*0 + 0.5*1 + 0.3*0 + 0.4*1 = 1.6
5. 阈值
- 阈值是决定感知机是否激活(输出1)的临界值,未达到时保持未激活状态(输出0)
- 本例设定的阈值为:
1.5
6. 激活函数
- 感知机在完成加权求和后,将结果输入激活函数
- 其核心作用是在输出中引入非线性特性,根据聚合输入值决定感知机是否激活。
- 激活函数的判断逻辑很简单:
(sum > treshold) == (1.6 > 1.5)
感知机输出机制
感知机的最终输出是激活函数的计算结果,代表基于输入和权重做出的决策判断。
激活函数将加权和映射为二进制值(1或0),可理解为"是/否"或"真/假"。
本例输出为1,因为:(sum > treshold) == true
感知机学习机制
感知机能够通过训练过程从样本中学习。
感知机在训练过程中会根据误差信号调整权重参数,通常采用感知机学习规则或反向传播算法来完成这一过程。
感知机的学习过程通过标注样本进行训练:首先输入已知期望输出的样本数据,然后将实际输出与期望输出进行比对,最后根据误差信号动态调整权重参数,从而逐步缩小预测输出与期望输出之间的误差。
通过这种学习机制,感知机能够自主优化权重参数,从而获得对未知输入数据做出准确预测的能力。
提示:单靠单个神经元无法完成复杂决策,需要其他神经元提供更多输入因素,例如:艺人水平是否达标?天气条件是否理想?(其他相关因素)这种情况下可以采用多层感知机(MLP)来实现更复杂的决策功能。
需要强调的是,虽然感知机在神经网络发展史上具有开创性意义,但其本质上是线性分类器,只能处理线性可分的数据模式。不过,当我们将多个感知机分层组合,并配合非线性激活函数时,就能构建出可以学习复杂非线性关系的深度神经网络。
神经网络
感知机是迈向神经网络的第一步,演进关系:单层感知机 → 多层感知机(MLP) → 深度神经网络(DNN)
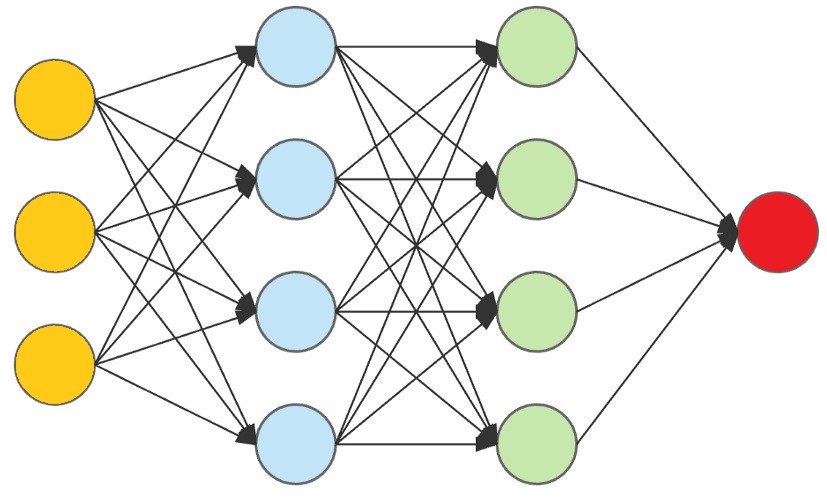
感知机通常作为构建更复杂神经网络的基础组件,例如多层感知机(MLP)或深度神经网络(DNN)。
通过将多个感知机分层组合并构建神经网络结构,这些模型能够学习并表征数据中的复杂模式和关联关系,从而支持图像识别、自然语言处理和决策制定等任务。
反馈提交成功
感谢您的反馈,我们将尽快处理您的反馈

